| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 |
- Spring XD
- Clean Code
- 일본 백패킹
- 제주
- Spring Boot
- hdfs
- Spring
- design pattern
- Linux
- Java
- 스프링 배치
- 인텔리J
- Storm
- 도메인주도설계
- apache storm
- SBT
- Hbase
- Gradle
- docker
- DDD
- 엘라스틱서치
- 구마모토 백패킹
- intellij
- Spring Batch
- nginx
- Angular2
- elastic search
- scala
- elasticsearch
- hadoop
- Today
- Total
욱'S 노트
모노이드/Monoid (Kotlin 함수형 프로그래밍 #9) 본문
범주(Category)
범주란 대상(Object)과 사상(Morphism)의 모음
항등사상: 대상 A에 대한 항등 사상(id_A)가 존재해야 한다. 이 사상은 A에서 A로 가는 사상
사상의 연속성: f: A→B와 g: B->C가 주어졌을때, 두 사상의 합성 g∙f: A→C가 존재해야 한다. 두 사상을 연결하여 하나의 사상으로 만들 수 있어야 한다.
합성의 결합법칙: 세 개의 사상 f,g,h가 주어졌을때, (h∙g)∙f = h∙(g∙f)가 성립해야 한다. 사상을 연결할 때 순서가 중요하지 않다.
대상은 수학적으로는 집합이며 프로그래밍에서 익숙한 용어로 바꾸면 타입이다. 예를 들어 정수 타입은 모든 정수를, 부울 타입은 참과 거짓 만을 포함한다.

사상은 화살표(arrow)이다. 화살표는 두 대상 사이의 관계를 나타낸다. 프로그래밍에서는 화살표는 함수, 변환, 매핑 등이 될 수 있다.
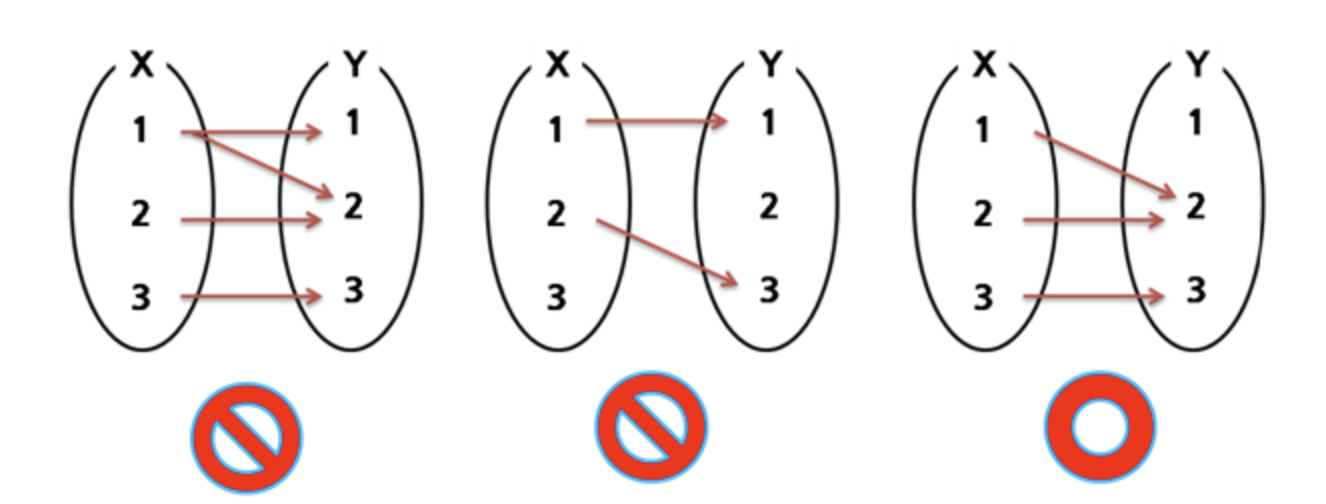
코드로 나타내는 아래와 같다.
interface Category<T> {
fun identity(x: T): (T) -> T
fun <A, B, C> compose(f: (A) -> B, g: (B) -> C): (A) -> C
}
fun main() {
val stringCategory = object : Category<String> {
override fun identity(x: String): (String) -> String = { x }
override fun <A, B, C> compose(f: (A) -> B, g: (B) -> C): (A) -> C = { a: A -> g(f(a)) }
}
val f = { s: String -> s.toUpperCase() }
val g = { s: String -> "$s!" }
val h = { s: String -> s.repeat(2) }
val left = stringCategory.compose(stringCategory.compose(f, g), h) // (f•g)•h
val right = stringCategory.compose(f, stringCategory.compose(g, h)) // f•(g•h)
println(left("hello")) // HELLO!HELLO!
println(right("hello")) // HELLO!HELLO!
}
범주론은 추상적인 수학구조로, 대상과 사상의 모음인 범주를 다루는 학문이다. 범주론은 함수형 프로그래밍에 적용할 수 있는데, 대상은 타입, 데이터구조, 모듈과 같은 개념으로, 사상은 화살표(함수, 변환, 매핑)으로 나타낼 수 있다.
모노이드 (Monoid)
추상대수학에서 모노이드(영어: monoid)는 항등원을 갖는, 결합 법칙을 따르는 이항 연산을 갖춘 대수 구조이다. 군의 정의에서 역원의 존재를 생략하거나, 반군의 정의에서 항등원의 존재를 추가하여 얻는다.
모노이드 (𝑀,⋅)는 다음과 같은 데이터로 구성되는 대수 구조이다.
이 데이터는 다음과 같은 두 공리를 만족시켜야 한다.
- (결합 법칙) 임의의 𝑎,𝑏,𝑐 ∈ 𝑀에 대하여, (𝑎⋅𝑏)⋅𝑐 = 𝑎⋅(𝑏⋅𝑐)
- (항등원의 존재) 임의의 𝑎 ∈ 𝑀에 대하여 1⋅𝑎 = 𝑎⋅1 = 𝑎가 성립하는 원소 1∈𝑀이 존재한다. (만약 이러한 항등원이 존재한다면, 이는 유일하다는 것을 쉽게 보일 수 있다.)
두 번째 공리를 생략하면 반군(SemiGroup)의 개념을 얻는다. 즉, 모노이드와 반군의 관계는 환과 유사환의 관계와 같다. 보통, 편의상 이항 연산을 (곱셈과 같이) 생략하는 경우가 많다.
즉, 다음과 같은 포함 관계가 성립한다.
마그마 ⊋ 반군 ⊋ 모노이드 ⊋ 군 (범주(Category) · 마그마 · 반군(Semigroup) · 모노이드 · 준군 · 아벨 군 · 위상군 · 리 군)
범주론적으로, 모노이드는 집합과 함수의 범주 Set 속의 모노이드 대상이다. 또한, 하나의 대상만을 갖는 작은 범주는 모노이드와 같은 개념이다. 이 경우, 모든 사상은 자기 사상이며, 모노이드 이항 연산은 자기 사상의 합성이다.
(대상) 집합 (Set): 원소들의 모음.
(사상) 이항 연산 (Binary operation): 두 원소를 입력받아 집합의 다른 원소를 반환하는 연산. 이 연산은 해당 집합내에서만 이루어진다. f: S X S → S로 정의. 대표적인 이항연산은 덧셈,곱셈,나눗셈이 있다.
(사상으로서 만족해야될 요구사항)
결합법칙(Associativity) : 모든 원소 a,b,c에 대해서 (a•b)•c = a•(b•c)가 성립해야한다. 즉 연산의 순서과 결과에 영향을 주지 말아야 한다. (1 + 2) + 3 = 1 + (2 + 3) = 6과 같이 덧셈 연산은 결합 법칙이 성립한다.
항등원(Identity element): 이항 연산에서 특별한 역할을 하는 원소로 집합 S의 모든 원소 a와 연산을 수행한 결과가 a가 자기 자신이여야 한다. 집합 S의 항등원라고 e라고 하면 e•a = a•e = a이다. 예를 들어 덧셈연산의 항등원은 0이고, 곱셈연산의 항등원은 1이다.
코드로 보면 다음과 같다.
interface Monoid<A> {
fun combine(a1: A, a2: A): A
val nil: A
}
val stringMonoid = object : Monoid<String> {
override fun combine(a1: String, a2: String): String = a1 + a2
override val nil: String = ""
}
val intAddition = object: Monoid<Int> {
override fun combine(a1: Int, a2: Int): Int = a1 + a2
override val nil: Int = 0
}
val booleanAnd = object : Monoid<Boolean> {
override fun combine(a1: Boolean, a2: Boolean): Boolean = a1 && a2
override val nil: Boolean = true
}
val optionMonoid = object : Monoid<Option<A>> {
override fun combine(a1: Option<A>, a2: Option<A>): Option<A> = a1.orElse { a2 }
override val nil: Option<A> = None
}
모노이드의 combine 연산은 리스트 접기 연산에 잘 어울린다.
val words = listOf("Hic", "Est", "Index")
val rightResults = words.foldRight(stringMonoid.nil, stringMonoid::combine)
val leftResults = words.foldLeft(stringMonoid.nil, stringMonoid::combine)
fun <A, B> foldMap(la: List<A>, m: Monoid<B>, f: (A) -> B): B =
la.foldLeft(m.nil) { b: B, a: A -> m.combine(b, f(a)) }
val results = foldMap(words, stringMonoid, { it + "!" })
모노이드를 사용하면 균형접기(balanced fold)가 가능하다.
combine(a, combine(b, combine(c, d)))
combine(combine(a, b), combine(c, d))
균형 접기가 가능하다는 것은 병렬처리가 가능하다는 것이다.
fun <A, B> parFoldMap(
la: List<A>,
pm: Monoid<Par<B>>,
f: (A) -> B
): Par<B> =
when {
la.size >= 2 -> {
val (la1, la2) = la.splitAt(la.size / 2)
pm.combine(parFoldMap(la1, pm, f), parFoldMap(la2, pm, f))
}
la.size == 1 ->
unit(f(la.first()))
else -> pm.nil
}
정리
모노이드가 함수적 프로그래밍에 주는 이점
- Composability - 모노이드는 결합법칙이 성립하기 때문에 순서에 상관없이 작은 단위의 연산을 조합여서 더 큰 연산을 수행한다.
- Immutable - 모노이드는 접기(Foldable)에 잘 어울린다. 접기는 새로운 값을 생성하기 위해 기존 값을 변경하지 않는다.
- Parallelism - 모노이드는 결합법칙을 만족하므로, 병렬처리에 유리하다.
참고자료 : https://ko.wikipedia.org/wiki/%EB%B2%94%EC%A3%BC%EB%A1%A0
범주론 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 범주론(範疇論, 영어: category theory)은 수학 용어로, 수학적 구조와 그들 간의 관계를 범주(영어: category)라는 추상적인 개념으로써 다루는 이론이다. 어떠한 '구
ko.wikipedia.org
'Methdology > Functional Programming' 카테고리의 다른 글
| 모나드/Monad (Kotlin 함수형 프로그래밍 #10) (0) | 2025.02.07 |
|---|---|
| 모나드 소개/Introduction of Monad (Kotlin 함수형 프로그래밍 #8) (4) | 2025.01.22 |
| 컴파일타임 디펜던시 인젝션/Compile Time Dependency Injection (Kotlin 함수형프로그래밍 #8) (4) | 2025.01.21 |
| 도메인 모델링/Domain Modeling (Kotlin 함수형 프로그래밍 #7) (3) | 2025.01.20 |
| 외부효과와 입출력/Effects and IO (Kotlin 함수형프로그래밍 #6) (0) | 2025.01.17 |

